what does it mean to fit a model

Model Plumbing equipment

In this lesson we'll cover how to fit a model to data using matlab's minimization routine 'fminsearch'. Model plumbing fixtures is a procedure that takes three steps:

First you need a role that takes in a prepare of parameters and returns a predicted data set.

2nd you demand an 'error function' that provides a number representing the difference between your information and the model's prediction for any given ready of model parameters. This is normally either the sums of squared error (SSE) or maximum likelihood.

Tertiary you demand to detect the parameters that minimize this difference. Once you lot set things up properly, this 3rd step is easy thanks to the nerds at Mathworks.

Contents

• One parameter example - Weber's constabulary
• Stride 1: model prediction
• Step 2: Comparison the model prediction to the data
• Step 3: Finding the best fitting parameter
• Other measures of fault
• Model plumbing fixtures weighting by standard error of the mean.
• Model fitting weighting by private measurements.
• Model fitting with more than one parameter.
• Holding variables constant while fitting.
• Other notes.

I parameter example - Weber'due south constabulary

We'll start with a simple example where our model has only one parameter. Weber's police force states that the ability for a subject to discover an increase in stimulus intensity is proportional to the starting, or baseline intensity. That is, if x is the stimulus intensity, the increase threshold is kx, where thou is the 'Weber fraction'. This fraction is our i parameter.

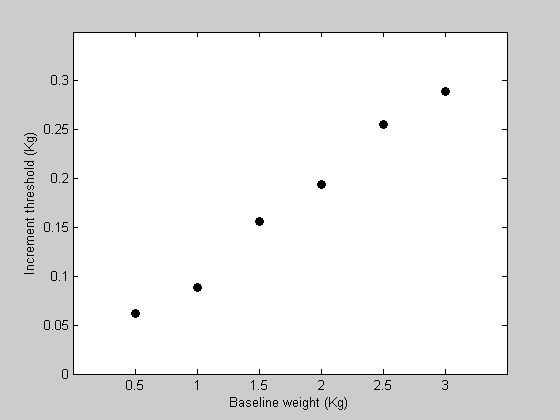
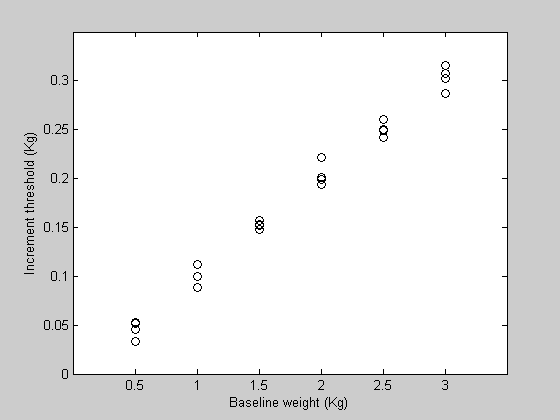
Suppose that nosotros ran an experiment testing the ability for a field of study to detect an increase in the weight of an object held in the hand. Subjects were given starting weights (in Kg) of the following values:

clear          all          x = [.5,one,1.5,2,two.five,3];        

Increment thresholds are defined here as the increase in weight that tin be detected correctly 80% of the time. This would use a psychophysical method such as 'two-alternative forced-choice' (2AFC) that we don't need to deal with right here. Let the corresponding increase thresholds for a subject be:

y = [  0.0619    0.0888    0.1564    0.1940    0.2555    0.2890];   effigy(ane) clf h1=plot(x,y,'ko','MarkerFaceColor','k'); set(gca,'YLim',[0,0.35]); set(gca,'XLim',[0,three.five]); set up(gca,'XTick',x) xlabel('Baseline weight (Kg)'); ylabel('Increase threshold (Kg)');        

Step 1: model prediction

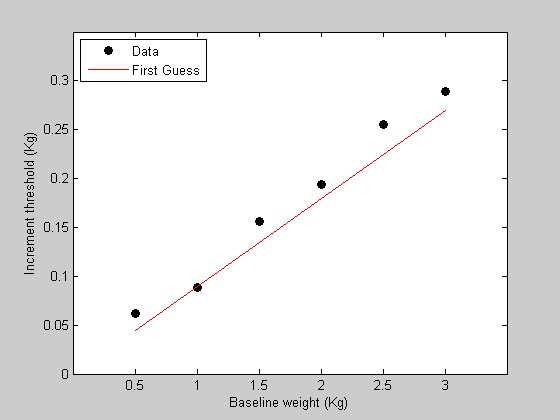
Nosotros're at present set up for the outset footstep - writing the function containing the model that predicts the data. This role needs to accept in a unmarried parameter and the baseline weights and return a prediction of the data. The parameter is the WeberFraction which is the slope of the line of the data in figure one.

Nosotros'll utilise a specific convention for how we stand for our parameters which is to place them inside a single structure. With one parameter this seems a little light-headed, but it'll make sense when we add together more than parameters.

Here's a structure containing a starting gauge at the Weber fraction 'w':

startingW  =0.09;   p.westward = startingW;        

Our function 'predictWeight' is a single line function that volition take in this structure as its commencement statement, and the list of baseline values as the second statement:

                  pred = WebersLaw(p,10);        

plot the prediction

hold          on          h2=plot(x,pred,'r-'); legend([h1,h2],{'Data','First Estimate'},'Location','NorthWest');        

Step ii: Comparing the model prediction to the information

Fourth dimension for step 2. Hither's a two-line function 'WebersLawErr' that calculates the sums of squared error between the model's prediction and the data:

            err = WebersLawErr(p,x,y)        

err =      0.0022        

Stride 3: Finding the best fitting parameter

What is the all-time plumbing fixtures Weber fraction? With one parameter we can visualize this problem by calculating the error of the fits for a range of Weber fractions:

WeberList = linspace(0.08,0.12,41); errList = zeros(size(WeberList));          for          i=1:length(WeberList)     p.w = WeberList(i);     errList(i) = WebersLawErr(p,x,y);          end          figure(2) clf plot(WeberList,errList,'k-'); xLabel('Weber fraction'); yLabel('SSE');        

Nosotros can plot the fault value of our initial guess in red:

hold          on          plot(startingW,err,'ro','MarkerFaceColor','r');        

It looks like the all-time fitting Weber fraction is between 0.095 and 0.i. We could go farther and keep sampling finer and finer in this range to discover a minimum value. But this is a very inefficient way to notice the minimum of a function. It's particularly bad if there are multiple parameters to fiddle with.

Fortunately, matlab has a function 'fminsearch' that uses a sophisticated numerical analysis technique that can find the minimum of a function like this - as long as it's reasonably continuous and well behaved. I observe Matlab's usage of fminsearch to be a fleck kludgy and awkward, then I've written my own function that calls 'fminsearch' that I find easier to use. Information technology'south called 'fit.m', and it works like this:

assistance          fit        

          [params,err] = fit(funName,params,freeList,var1,var2,var3,...)    Helpful interface to matlab's 'fminsearch' part.    INPUTS   'funName':  role to be optimized.  Must have grade err = <funName>(params,var1,var2,...)   params   :  structure of parameter values for fitted function       params.options :  options for fminsearch programme (see OPTIMSET)   freeList :  Cell assortment containing list of parameter names (strings) to be complimentary in fi   var<n>   :  extra variables to be sent into fitted function    OUTPUTS   params   :  structure for best fitting parameters    err      :  mistake value at minimum    See 'FitDemo.thou' for an instance.    Written by Geoffrey M. Boynton, Summer of '00      Overloaded methods:        gmdistribution/fit        

The commencement statement that 'fit' needs is the name of the office to exist minimized, equally a string. In our case it'due south 'WeberListErr'. This function has to take the convention that it'south get-go argument is a structure containing the model parameters, and that the commencement argument information technology returns is the error value. The function can accept in additional arguments too, in any order.

The second argument into 'fit' is a construction containing a starting set of parameters. This is the kickoff guess for where the minimum is, and it tin can make a difference in the power for fminsearch to find the overall minimum.

The third argument is a jail cell array containing a list of parameters that we will let to vary to notice the minimum. The cell array is a list of strings containing fields of the names of the parameters in our construction. In our case, it's simply a single field named 'w'.

The remaining arguments into fit are the remaining arguments that the function to be minimized needs, starting with the second argument. In our case they are the parameters x and y, in proper order.

The outset argument in the output of 'fit' is a structure containing the best-fitting parameters. The 2d argument is the error associated with these values.

Allow's go!

[bestP,bestErr] = fit('WebersLawErr',p,{'w'},x,y);        

Fitting "WebersLawErr" with 1 free parameters.        

'bestP' is a construction containing the parameters that minimized the SSE betwixt the information and the model.

bestP        

bestP =       w: 0.0988        

We tin plot this in effigy 2

hold          on          plot(bestP.westward,bestErr,'bo','MarkerFaceColor','b');        

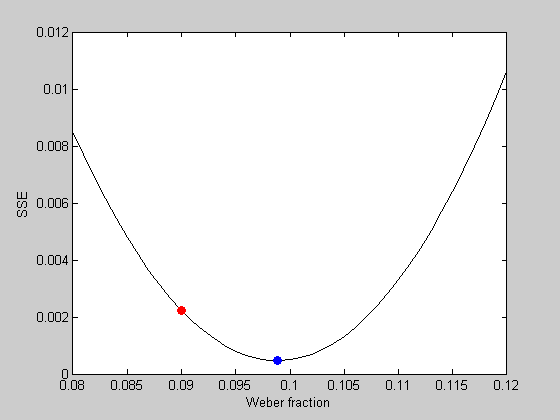
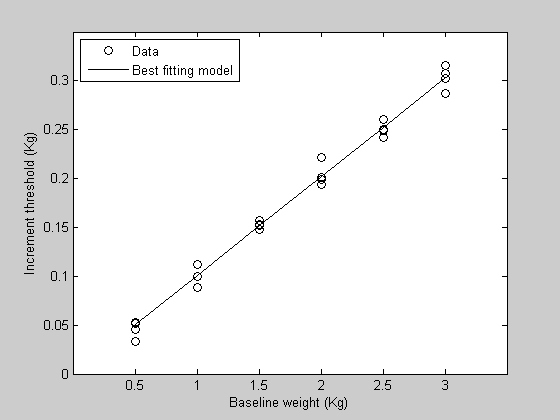
See how it sits on the bottom of the bend? We found the optimal Weber fraction that fits our data. About 0.1033 (or 10.3%)

Finally, we'll go the model prediction using this best plumbing fixtures value and plot the predictions with the information in effigy i

bestPred = WebersLaw(bestP,x); effigy(1) h3=plot(x,bestPred,'b-'); legend([h1,h2,h3],{'Information','Beginning Guess','All-time Value'},'Location','NorthWest');        

Other measures of error

The best plumbing equipment parameters tin can depend strongly on your pick of mistake function. For our example, another way to state Weber's police is that the ratio of the increment thresholds and the baseline values is constant. So some other measure of the Weber fraction is the hateful of these ratios across baselines:

meanRatio  = hateful(y./ten)    disp(sprintf('Best w: %five.4f, mean ratio: %5.4f',bestP.due west,meanRatio));        

meanRatio =      0.1021  All-time due west: 0.0988, mean ratio: 0.1021        

This difference is at least in function acquired by a greater weight for the mean ratio on the lower baseline values (or equivalently a greater weight for the high baseline values for the model). It's non obvious which is more valid. The model puts equal weight on accented errors in the 'y' dimension across baselines, while the mean ratio puts equal weights on the ratios beyond baselines.

Model fitting weighting by standard error of the mean.

The mean ratios might be a better method because thevariability in the information (which nosotros haven't yet talked most) probably increases with the baseline. So errors at high baselines are less meaningful than at depression baselines.

A natural fashion to right for variance in the data is to normalize the SSE by the standard error of the mean for each data signal. Then our fault value will represent a total error in sqsuared standard error units.

Let the standard error of the mean of our estimates exist:

s =  [ 0.016    0.0216    0.0140    0.0225    0.0183    0.0517];    figure(1) h=errorbar(x,y,s,'k','LineStyle','none');        

Next, edit the 'WebersLawErr' function to this:

                       [bestPsem] = fit('WebersLawErr',p,{'w'},x,y,s);    bestPredsem = WebersLaw(bestPsem,x); effigy(1) h4 = plot(x,bestPredsem,'yard-'); legend([h1,h2,h3,h4],{'Information','Showtime Approximate','Best fit using SSE','Best fit using standard errors'},'Location','NorthWest');        

Fitting "WebersLawErr" with ane free parameters.        

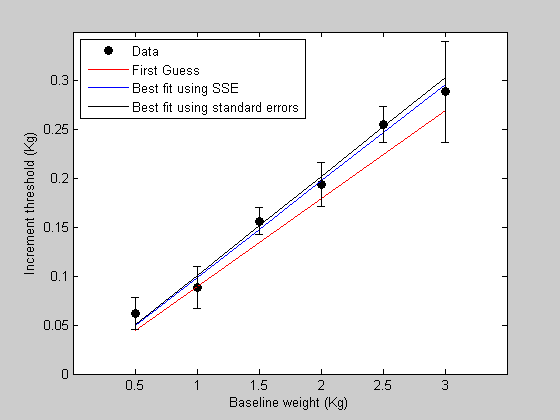
The new best fit takes into account the error bars so that data points with smaller mistake confined are weighted more heavily. You tin can think of this equally making the model prediction overlap more with the error bars, rather than but trying to get shut to the data points.

In this example, the final data signal (highest baseline value) is noisy, so the model's constraint to fit this point is relaxed. This causes the best fitting Weber fraction to change so that the prediction moves away from this noisy data indicate.

Model plumbing equipment weighting past individual measurements.

Another mode to account for the variability in your measurements is to use an error function that sums upwards the errors with respect to each individual measurements, rather than the means. This is closely related to the previous method - it's identical in the limit equally you add more and more measurements to each mean.

We'll offset with a new sample data fix from the Weber's police experiment that has four measurements for each baseline intensity. We'll call the variable 'yy' instead of 'y'.

yy=[0.0457    0.0885    0.1533    0.1941    0.2607    0.3029;     0.0333    0.1119    0.1517    0.2218    0.2506    0.2866 ;     0.0513    0.1119    0.1481    0.1986    0.2490    0.3071 ;     0.0529    0.0996    0.1573    0.2011    0.2417    0.3162];        

Each of the 4 rows corresponds to a separate measurement across the 6 baseline values.

An easy way to compare these values to the model'due south prediction is to make the model predict a data set that's the same size as yy. This can be done by using a matrix xx that'due south the same size besides:

xx = repmat(x,four,ane)        

xx =      0.5000    1.0000    1.5000    2.0000    2.5000    iii.0000     0.5000    1.0000    one.5000    2.0000    2.5000    3.0000     0.5000    1.0000    1.5000    2.0000    two.5000    3.0000     0.5000    1.0000    ane.5000    2.0000    two.5000    3.0000        

We tin can plot this new data ready every bit individual data points:

effigy(3) clf h1=plot(xx,yy,'ko') fix(gca,'YLim',[0,0.35]); ready(gca,'XLim',[0,3.v]); prepare(gca,'XTick',x) xlabel('Baseline weight (Kg)'); ylabel('Increment threshold (Kg)');        

h1 =    528.0250   936.0029   937.0029   938.0029   939.0029   940.0029        

Information technology turns out that we've written our model office 'WebersLaw' so that it can take in matrices also as vectors, and then it will also make a predicted data set that'due south a matrix:

pred = WebersLaw(p,xx)        

pred =      0.0600    0.1200    0.1800    0.2400    0.3000    0.3600     0.0600    0.1200    0.1800    0.2400    0.3000    0.3600     0.0600    0.1200    0.1800    0.2400    0.3000    0.3600     0.0600    0.1200    0.1800    0.2400    0.3000    0.3600        

We've also written our fault function 'WebersLawErr' so that it tin calculates the SSE betwixt the elements of two matrices as well as vectors, since nosotros unwrapped our variables using the '(:)' method:

err = WebersLawErr(p,xx,yy)        

err =      0.0346        

This means that our fitting routine will work as well:

bestP = fit('WebersLawErr',p,{'west'},twenty,yy);        

Plumbing equipment "WebersLawErr" with ane free parameters.        

To get a prediction of the model with this best-plumbing fixtures value of w, nosotros only demand a unmarried vector instead of the whole matrix. Nosotros can do this by sending in the variable 'x' instead of 'twenty' in to 'WebersLaw':

pred = WebersLaw(bestP,10);        

Plot it:

agree          on          h2=plot(x,pred,'k-'); legend([h1(1),h2],{'Information','Best fitting model'},'Location','NorthWest');        

Model fitting with more than ane parameter.

Fitting a model that has more than one parameter is easy, since the hard office of really finding the all-time parameters is all done by Matlab's fminsearch function. Hither's an instance of a data gear up that needs a two-parameter model to fit it.

Suppose we're measuring the firing rate of a neuron while it is recovering from an adapted state. Permit 't' exist time in seconds, and 'y' be the firing charge per unit of the neuron. Here'south an example data gear up:

t = [0:10];   y=  [0.4346    9.8079   14.2634   xviii.2656   23.4209   27.8469   27.5358          ...          29.4886   26.4415   28.2591   32.8832];        

Plot the data

effigy(5) clf h1=plot(t,y,'ko','MarkerFaceColor','thou'); xlabel('Time (min)'); ylabel('Firing rate (Hz)');        

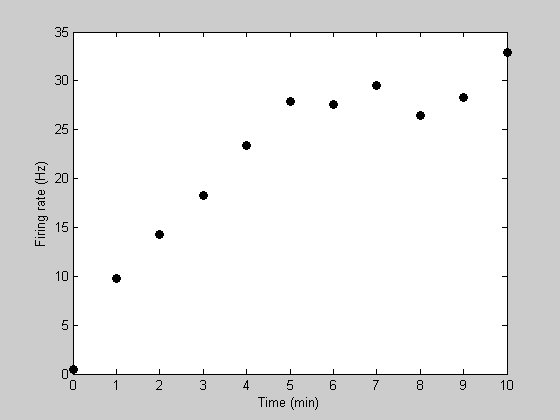
Notice how the recovery from adaptation starts out quickly and so asymptotes to a firing rate of almost 30Hz. A standard model for this sort of asymptotic role is an exponential. This can exist described with two parameters - one describing the asymptotic firing rate (we'll telephone call information technology 'rMax') and a second one decribing the rate of recovery (we'll call it 'k').

We need to do steps 1 and ii now from above - write the role containing the model and write a function comparing the model to the information. This time we'll practise information technology a piddling differently and combine the 2 into a single office, called 'predRecoveryErr':

This function returns the mistake value as the first parameter and the model prediction equally the 2d. The third input parameter - the information - is optional. If information technology isn't provided, then no comparison is fabricated to the data and a NaN is returned for the fault. This way, the same function can serve both every bit a mode to become model predictions, and to feed into 'fit.m' to notice the best fitting parameters.

Find that the model itself is simply one line again: p.rMax*(i-exp(-p.k*t))

We're ready to use this function to predict and fit data.

Intial parameters:

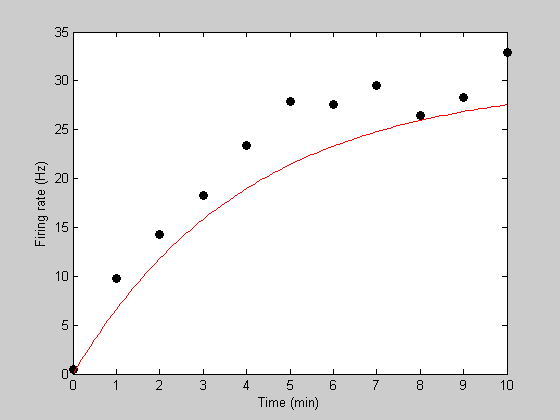
clear          p          p.m = .25; p.rMax = 30;        

Initial model prediction. Let'southward get fancy and use a higher sampling rate in time for the model prediction to get a smoother bend. Instead of predicting with the variable 't', we'll use:

tPlot = linspace(0,10,101);  [tmp,pred] = predRecoveryErr(p,tPlot);  hold          on          h2=plot(tPlot,pred,'r-');        

Intial error value:

err = predRecoveryErr(p,t,y)        

err =    154.4481        

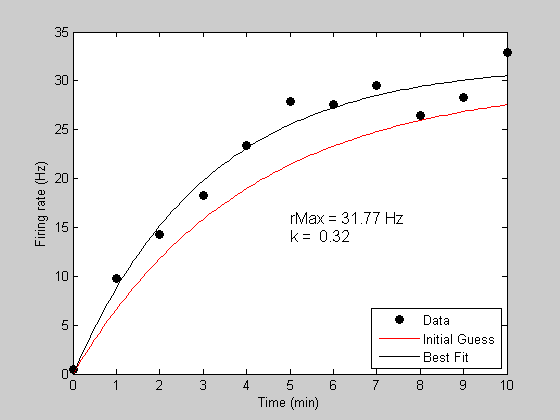
Find the all-time fitting parameters:

Our phone call to 'fit' will exist just as in the one parameter example, except that we'll listing two parameters in our cell array (3rd statement into 'fit'):

bestP = fit('predRecoveryErr',p,{'k','rMax'},t,y);        

Fitting "predRecoveryErr" with 2 free parameters.        

At present we'll get the best fitting prediction and plot it in black

[bestErr,bestPred] = predRecoveryErr(bestP,tPlot);  h3=plot(tPlot,bestPred,'k-');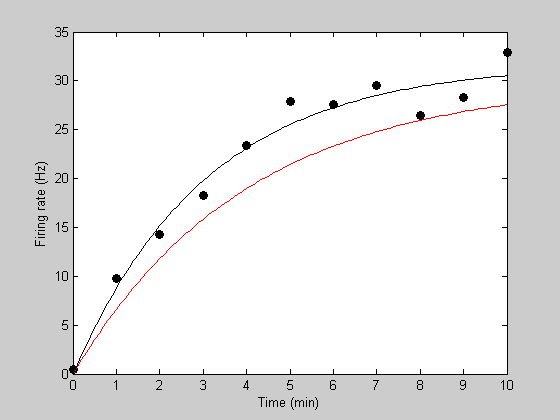        

Show the parameter values on the plot:

text(5,15,sprintf('rMax = %5.2f Hz\nk = %5.2f',bestP.rMax,bestP.k),'HorizontalAlignment','left','FontSize',12); legend([h1,h2,h3],{'Data','Initial Guess','Best Fit'},'Location','SouthEast');        

Property variables abiding while fitting.

The 'fit' role lets you easily fit with a subset of parameters. Suppose that you lot know that the asymptotic firing rate is 30Hz, and we just want to permit the parameter '1000' vary. We do this by only list 'thousand' as a free parameter in third argument to 'fit':

bestPK = fit('predRecoveryErr',p,{'k'},t,y); [bestErrK,bestPredK] = predRecoveryErr(bestPK,tPlot);  h4 = plot(tPlot,bestPredK,'b-'); legend([h1,h2,h3,h4],{'Data','Initial Guess','All-time Fit','Best westward/ rMax = 30'},'Location','SouthEast');        

Fitting "predRecoveryErr" with i free parameters.        

Other notes.

'fit' allows parameters for your model to be vectors equally well. For example, if you had a model with parameters:

p.x = [2,four,vi];        

You lot could permit all three values in x to be free by using {'ten'} as your list of free parameters. If you want only the first element to be free, use {'10(1)'}. For just the first and 3rd, you tin utilize {'x([i,iii])'}, or {'x(1)','x(iii)'}. Either will work.

mccabesheizips.blogspot.com

Source: https://courses.washington.edu/matlab1/ModelFitting.html

Share this post