Art of the Fourth Dimension Shipping Exhibiting and Lending Timebased
The painter who entered the time

A 1954 painting by Salvador Dalí features a mysterious, 4-dimensional 'hypercube'. Fiona Macdonald finds out how maths fascinated the great Spanish painter.
West
When mathematician Thomas Banchoff received a message in 1975 asking him to contact Salvador Dalí, his colleague told him: "It'south either a hoax or a law suit." Yet it turned out to be the get-go of a collaboration that lasted most a decade. Each year, Dalí visited New York and called on the Chocolate-brown University professor for advice, setting him challenges for artworks that he hoped one 24-hour interval to consummate – including a statue of a equus caballus fabricated up of three parts that were kilometres apart.
The Castilian artist had long found inspiration in science. He wrote in his 1958 Anti-Matter Manifesto: "In the Surrealist catamenia I wanted to create the iconography of the interior earth and the world of the marvellous, of my father Freud… Today the exterior globe and that of physics, has transcended the one of psychology. My father today is Dr Heisenberg."
Although Dalí continued to explore ideas of theoretical physics until his death in 1989, arguably the greatest expression of his scientific curiosity came in the grade of a 1954 painting. Hovering eerily in the air above a figure modelled by Dalí's married woman Gala, Jesus Christ appears in a pose that has been painted by artists for centuries. Yet there are no nails in this epitome of crucifixion, and the cross is non fabricated of forest. It's not even in a dimension we tin can run across.

By breaking out of three dimensions, Crucifixion (Corpus Hypercubus) establish new meaning in a traditional biblical scene (Credit: Globe History Archive/Alamy Stock Photograph)
Crucifixion (Corpus Hypercubus) unites a classical portrayal of Christ with a shape that merely exists in mathematical theory. Dalí'southward floating cantankerous is what Banchoff describes equally "an unfolded 4-dimensional cube". In a 2012 lecture given at the Dalí Museum, Banchoff explains how the creative person was trying to use "something from a three-dimensional world and accept it beyond… The exercise of the whole thing was to exercise two perspectives at once – two superimposed crosses."
Sculptures of the listen
Just every bit the sides of a cube can be unfolded into six squares, a tesseract – or iv-dimensional cube – can be unfolded into eight cubes. While it's difficult to grasp, the thought of multiple dimensions allows scientists to envisage shapes that mathematician Marcus du Sautoy calls "sculptures of the mind". Every bit he argues in his Radio 3 programme The Secret Mathematician, "Information technology's not possible to see a 4D cube in our limited 3D universe, but in that location are different means to imagine i."
Dalí's ain 'sculpture of the heed' brings geometry into the realm of the metaphysical. "In that location is a meditative intensity to Crucifixion (Corpus Hypercubus)," says fine art critic and poet Kelly Grovier. "The painting seems to take cracked the link between the spirituality of Christ's salvation and the materiality of geometric and physical forces. It appears to bridge the divide that many feel separates science from religion."

Salvador Dalí worked on his painting Crucifixion (Corpus Hypercubus) for four years – this photo was taken in 1951 (Credit: Francesc Catala-Roca)
By breaking out of iii dimensions, the creative person could find new meaning in a traditional biblical scene, argues du Sautoy. "The idea of the time existing across our cloth world resonated for Dalí with the spiritual world transcending our physical universe."
The shape of things to come
A 4th dimension in art seemed for many a natural evolution. In his 1936 Dimensionist Manifesto, Hungarian poet and art theorist Charles Tamkó Sirató claimed that artistic evolution had led to "Literature leaving the line and entering the airplane… Painting leaving the airplane and entering space… [And] sculpture stepping out of closed, immobile forms." Next, Sirató said, there would be "the artistic conquest of iv-dimensional infinite, which to engagement has been completely fine art-free".
Cubists like Pablo Picasso had already attempted to represent four-dimensional shapes on the two-dimensional sail, excited by the theories of 19th-Century mathematicians Bernhard Riemann and Henri Poincaré. Nonetheless Dalí looked farther dorsum for inspiration, describing his painting as "metaphysical, transcendent cubism". He claimed that Crucifixion (Corpus Hypercubus) was influenced by a 13th-Century mystic and a 16th-Century architect. "It is based entirely on the Treatise on Cubic Form by Juan de Herrera, Philip II's architect, architect of the Escorial Palace; it is a treatise inspired by Ars Magna of the Catalonian philosopher and alchemist, Raymond Lull."
According to Banchoff, "Lull was a Catalonian who studied two dimensions; ii centuries later Herrera took that to the third dimension. Here's Dalí in a straight line, taking it up to the fourth dimension." The Brown University professor can also meet a link betwixt Dalí's hypercube and drawings of crosses made by those studying perspective in the 18th Century, such as the French astronomer Edme-Sebastien Jeaurat. When Jeaurat and others were drawing these shapes in 1750, says Banchoff, they "were not thinking of it as an unfolded iv-dimensional cube – that came 1 or two centuries afterward".
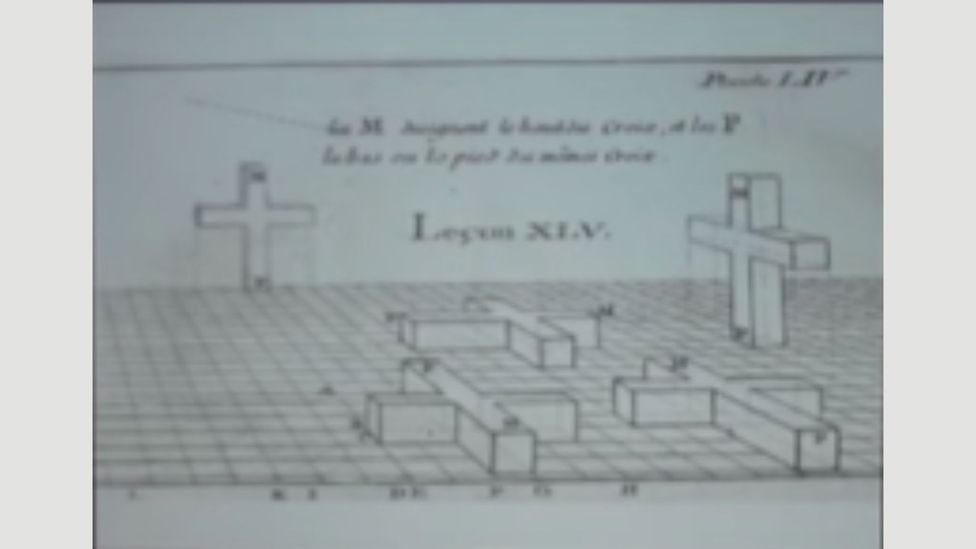
Thomas Banchoff recognised the shape of an unfolded 4-dimensional cube in this sketch past French astronomer Edme-Sebastien Jeaurat (Credit: YouTube)
Notwithstanding Banchoff recognised the shape equally soon equally he saw Jeaurat'southward sketches. "I said: 'That's information technology. That'southward the 4D unfolded cross. That's the Corpus Hypercubus.'" Dalí was able to enter the fourth dimension with the help of astronomers and mystics every bit well as mathematicians.
And he brought with him the fears of his age. "Corpus Hypercubus was non an piece of cake problem to solve," says Banchoff. "Information technology took him four years… earlier he was satisfied with the painting." Crucifixion (Corpus Hypercubus) was completed in 1954: the year Cern in Geneva was founded. "Cold War fears of nuclear anything were accelerating," says Grovier. "Atomic structure, in other words, was on everyone's mind and how tampering with such mysteries might bring about either our devastation or survival."
For Dalí, geometry could be a route to eternal salvation. "In Dalí's work, atomism and scientific discipline appear to be the very fabric on which redemption and salvation are stitched," says Grovier. "The tesseractic crucifix would seem to extend beyond the dimensions of this earth into planes unknown."
It's something the artist himself acknowledged. As he said in The Dalí Dimension, "Thinkers and literati can't give me anything. Scientists give me everything, even the immortality of the soul."
If y'all would like to annotate on this story or anything else you lot accept seen on BBC Culture, head over to our Facebook folio or message us on Twitter .
And if you liked this story, sign upward for the weekly bbc.com features newsletter , called "If You But Read half-dozen Things This Week". A handpicked option of stories from BBC Time to come, Earth, Culture, Capital, Travel and Autos, delivered to your inbox every Fri.
Source: https://www.bbc.com/culture/article/20160511-the-painter-who-entered-the-fourth-dimension
0 Response to "Art of the Fourth Dimension Shipping Exhibiting and Lending Timebased"
Post a Comment